Abstract: We introduce a stochastic graph-based method for computing relative importance of textual units for Natural Language Processing. We test the technique on the problem of Text Summarization (TS). Extractive TS relies on the concept of sentence salience to identify the most important sentences in a document or set of documents. Salience is typically defined in terms of the presence of particular important words or in terms of similarity to a centroid pseudo-sentence. We consider a new approach, LexRank, for computing sentence importance based on the concept of eigenvector centrality in a graph representation of sentences. In this model, a connectivity matrix based on intra-sentence cosine similarity is used as the adjacency matrix of the graph representation of sentences. Our system, based on LexRank ranked in first place in more than one task in the recent DUC 2004 evaluation. In this paper we present a detailed analysis of our approach and apply it to a larger data set including data from earlier DUC evaluations. We discuss several methods to compute centrality using the similarity graph. The results show that degree-based methods (including LexRank) outperform both centroid-based methods and other systems participating in DUC in most of the cases. Furthermore, the LexRank with threshold method outperforms the other degree-based techniques including continuous LexRank. We also show that our approach is quite insensitive to the noise in the data that may result from an imperfect topical clustering of documents.

Original Paper

Authors: Güneş Erkan, Dragomir R. Radev (University of Michigan), 2004

–

Paper Summary

Introduction

Goal: use sentence-based graphs on text summarization task

Text Summarization: process of automatically creating a compressed version of a given text that provides useful information for the user. In this paper, we focus on multi-document extractive generic text summarization, where the goal is to produce a summary of multiple documents about the same, but unspecified topic.

• Extractive summarization produces summaries by choosing a subset of the sentences in the original document(s).
• Abstractive summarization is when the information in the text is rephrased
• Although summaries produced by humans are typically not extractive, most of the summarization research today is on extractive summarization. Purely extractive summaries often give better results compared to automatic abstractive summaries.

Extractive Summarization

• Early research on extractive summarization is based on simple heuristic features of the sentences such as their position in the text, the overall frequency of the words they contain, or some key phrases indicating the importance of the sentences.
• A commonly used measure to assess the importance of the words in a sentence is the inverse document frequency, or idf, which is defined by the formula:
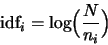
• More advanced techniques also consider the relation between sentences or the discourse structure by using synonyms of the words or anaphora resolution
• Researchers have also tried to integrate machine learning into summarization as more features have been proposed and more training data have become available

Approach

• Our summarization approach in this paper is to assess the centrality of each sentence in a cluster and extract the most important ones to include in the summary. We investigate different ways of defining the lexical centrality principle in multi-document summarization, which measures centrality in terms of lexical properties of the sentences.
• we present centroid-based summarization, a well-known method for judging sentence centrality. Then we introduce three new measures for centrality, Degree, LexRank with threshold, and continuous LexRank, inspired from the ``prestige’’ concept in social networks.

Sentence Centrality and Centroid-based Summarization

• Centrality of a sentence is often defined in terms of the centrality of the words that it contains.
• A common way of assessing word centrality is to look at the centroid of the document cluster in a vector space.
• The centroid of a cluster is a pseudo-document which consists of words that have tfxidf scores above a predefined threshold, where tf is the frequency of a word in the cluster, and idf values are typically computed over a much larger and similar genre data set.
• In centroid-based summarization, the sentences that contain more words from the centroid of the cluster are considered as central.

Centrality-based Sentence Salience

• Approach extractivce summarization using the conecept of prestige in social networks to assess sentence salience
• We hypothesize that the sentences that are similar to many of the other sentences in a cluster are more central (or salient) to the topic.
• Problem (1) How to define similarity between two sentences (2) How to compute the overall centrality of a sentence given its similarity to other sentences
  • Similarity: cosine similarity

Degree Centrality

• Since we are interested in significant similarities, we can eliminate some low values in the similarity matrix by defining a threshold so that the cluster can be viewed as an (undirected) graph, where each sentence of the cluster is a node, and significantly similar sentences are connected to each other.
• A simple way of assessing sentence centrality by looking at the graphs in Figure 3 is to count the number of similar sentences for each sentence. We define degree centrality of a sentence as the degree of the corresponding node in the similarity graph.
• The choice of cosine threshold dramatically influences the interpretation of centrality. Too low thresholds may mistakenly take weak similarities into consideration while too high thresholds may lose many of the similarity relations in a cluster.

Eigenvector Centrality and LexRank

• When computing degree centrality, we have treated each edge as a vote to determine the overall centrality value of each node
• However, in many types of social networks, not all of the relationships are considered equally important. As an example, consider a social network of people that are connected to each other with the friendship relation. The prestige of a person does not only depend on how many friends he has, but also depends on who his friends are.

• Degree centrality may have a negative effect in the quality of the summaries in some cases where several unwanted sentences vote for each other and raise their centrality. A straightforward way of avoiding this issue is to consider every node having a centrality value and distributing this centrality to its neighbors.

  

• p(u) is the centrality of node u
• adj[u] is the set of nodes that are adjacent to u

• deg(v) is the degree of the node v

• Can be written in matrix notation as

  

Page Rank

• matrix B is obtained from the adjacency matrix of the similarity graph by dividing each element by the corresponding row sum (row sum is equal to the degree of the corresponding node)
  • p^T is the left eignvector of matrix B
  • to guarantee p^T exists, B must be a stochastic matrix, and thus be able to be treated as a Markov chain. The centrality vector p corresponds to the stationary distribution of B.
• However, we need to make sure that the similarity matrix is always irreducible and aperiodic
  • To solve this problem, Page et al. suggest reserving some low probability for jumping to any node in the graph. This way the random walker can ``escape” from periodic or disconnected components, which makes the graph irreducible and aperiodic
  • If we assign a uniform probability for jumping to any node in the graph, we are left with the following modified version of Equation 3, which is known as PageRank where N is the total number of nodes in the graph, and d is a “damping factor” (0.1~0.2)

  

  

LexRank

• Unlike the original PageRank method, the similarity graph for sentences is undirected since cosine similarity is a symmetric relation.
• However, this does not make any difference in the computation of the stationary distribution. We call this new measure of sentence similarity lexical PageRank, or LexRank.

Continuous LexRank

• One improvement over LexRank can be obtained by making use of the strength of the similarity links.
• If we use the cosine values directly to construct the similarity graph, we usually have a much denser but weighted graph

Centrality vs. Centroid

• Graph-based centrality accounts for information subsumption among sentences.
• Graph-based centrality prevents unnaturally high idf scores from boosting up the score of a sentence that is unrelated to the topic.

My Thoughts

• SBERT extractive text summarization 에 사용되고 있는 알고리즘 이기 때문에 좀 오래된 이 논문을 한 번 읽어봤는데 요즘 쓰는 논문과 스타일이 확연하게 다르다. 더 친절하고 디테일한 느낌. 인트로에서 past work를 아웃라인 해주는 양이 다르다. 뭔가 더 교과서에 바로 들어가도 되는 느낌?ㅋㅋ 수포자인 나에게도 나름 반은 이해할 수 있도록 친절하게 식도 다 설명해주어서 좋았다. 그래도 완전히 이해는 못 했지만… markov chain, stochastic matrix에 대해서 조금 더 개인적으로 공부를 해야겟다는 생각이 들었다.
• 2004년에 쓰여진 논문이기 때문에 논문에서는 tf-idf 벡터만 사용한다. 그래서 굳이 따로 experimentation부분을 포함하지 않았다. 근데 여기 논문에서 한 실험에서는 threshold를 0.1로 설정하는 것이 appropriate하다고 써있는데 내가 실험하는 거에서는 0.4~0.5가 가장 좋은 결과를 보였다. 높지도 않고 낮지도 않은 그런 애매한 숫자… 어떻게 보면 너무 낮아도 안되고 너무 높아도 안 되기 때문에 가장 적합한 threshold인가? 그래도 확실히 논문을 좀 더 열심히 읽어보니까 threhold가 정확히 무슨 역할을 하고 있는지 알게 되어서 좋다.
• 또 이번 논문을 통해서 information retrieval의 정석인 page rank에 대해서도 대충 알게 된 거 같다. 개발을 계속 하고 싶다면 꼭 알아야하는 알고리즘 중 하나가 아닐까 싶다. 근데 이 부분을 정확히 이해를 못해서 유투브 영상을 따로 찾아봤다. 근데 더 찾아봐야할듯…ㅎㅎ;;